위와 같은 게임들은 분명한 것은 이기기 위해서 "나"는 내가 "최대"의 이익을 얻을 수 있는 방향으로 움직이며 "상대방"은 나의 이익이 "최소"로 하는 방향으로 움직여야한다. 그래야 서로가 이길 수 있으며 그런 방식으로 수읽기를 한다.
MinMax 알고리즘은 다음과 같이 구현될 수 있다. 아래 코드는 DFS이다.
Max_value(Node)는 v에 가장 작은 수로 넣어놓고 모든 노드를 탐색해서 가장 최대의 수를 찾는 것이고 Min_value(Node)는 v에 가장 큰 수를 넣어놓고 모든 노드 중 가장 작은 수를 찾는다. 이는 서로 Cross하면서 recursive하게 구현하는 것이 핵심이다.
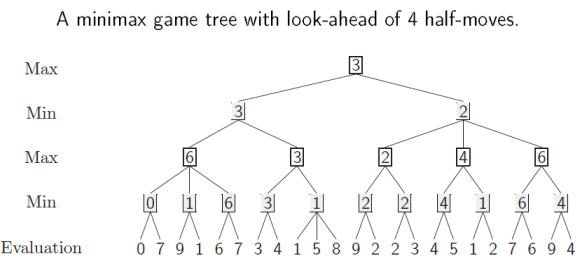
아래의 예를 보자.
Max는 "나"이고 다음 수에서 최대의 이익을 얻는 수를 둔다. Min은 "상대방"이고 "나"의 이익이 최소화 하는 수를 둔다. (서로 최선을 다한다는 가정하에)
그럼 결국 다음처럼 수 읽기를 하면 될 것이다.
탐색은 왼쪽에서 오른쪽으로 이루어진다고 하자.
이를 약간 발전시킨 방식이 Alpha-Beta pruning이다. (알파 베타 가지치기라고 부른다.)
필요없는 search를 없애는 즉 가지치는 방식으로 동작한다고 하여 Alpha-Beta pruning이다.
Alpha : 클수록 나에게 유리하다.
Beta : 작을수록 나에게 불리하다.
내 차례(Max)에서 beta cut : Value가 beta보다 크거나 같을 때, ( V >= beta )
상대방 차례(Min)에서 alpha cut : Value가 alpha보다 작거나 같을 때, ( V<= alpha )
왼쪽->오른쪽으로 탐색을 한다고 하면 Min의 경우에 2번째 depth(2->2,4,6)에서 2를 먼저 탐색을 했으니 나머지 4와 6은 볼 필요가 없으니 cut한다는 것이다.
알고리즘은 다음과 같다.

Maximum node에서 𝛼에 그 노드의 child 값 중에서 가장 큰 값을 저장하고, Minimum node에서 𝛽에 그 노드의 child 값 중에서 가장 작은 값을 저장한다.
만약 Minimum node k 에서 현재 𝛽 값이 𝛽 ≤ 𝛼 이 되면 root node에서 현재 node k 까지 경로에서 Maximum node의 가장 큰 값이 𝛼 가 되므로 node k 이하는 더 체크할 필요가 없다.
반대로 만약 Maximum node I 에서 현재 𝛼값이 𝛽 ≤ 𝛼 이 되면 root node에서 현재 node I 까지 경로에서 Minimum node의 가장 작은 값이 𝛽가 되므로 node I 이하는 더 체크할 필요가 없다.








댓글 없음:
댓글 쓰기