Cassandra stress-test를 활용한 Garbage Collector TEST (G1GC, CMS, ZING Read/Write Mixed)

Cassandra DB는 ring 구조의 db로서 hashing과 replication을 통해 성능(속도, 안전성)을 보장한다.

카산드라를 도입하기 위해서 스트레스 테스트를 해야할 때 카산드라 자체에서 지원하는 tool을 활용하면 쉽게 테스트가 가능하다.

본 포스팅은 카산드라 테스트 툴을 활용하여 가비지 컬렉터가 어떻게 동작하는지, 그리고 성능은 어떤지 보고자 한다.


gc는 서버의 메모리 스펙에 따라서 heap을 잘 조절해가며 최적화를 진행한다.
3대의 cassandra를 준비하고 각각의 GC 세팅을 다르게하여 테스트를 해보자.


서버 각각의 메모리는 32G이다.

그리고 java는 1.8(zulu jdk)를 썼고 zing test시에도 zing 1.8 version을 사용하였다.
후에 v11로 올려서 테스트해볼 예정이다.


테스트 하기전에 GC에 대해서 대략적으로 알아보자.

대부분의 객체는 life cycle이 짧다. 즉 객체는 빨리 소멸한다는 것이고 이런 객체들이 차지하고 있는 메모리를 잘 반환(청소)해야 할 것이다.

메모리에 객체가 할당되고 제거될 때에는 각각의 객체 size도 다르고 소멸주기도 다르기 때문에 결국 메모리 파편화가 발생하며 이는 새로운 객체가 할당될 때 문제가 된다. 마치 DB에서도 빈번한 insert/delete가 발생하면 인덱스에 페이지(블럭)의 순서가 꼬여서 단편화가 생기는 것과 같은 개념이다.


따라서 메모리 공간을 적절히 잘 나눌수만 있다면 그리고 그 메모리 공간 전체를 비울 수만 있다면 특별한 액션을 취하지 않아도 이 자체만으로 성능이 좋을 것이라는 추측이 가능하다.

하지만 GC가 발생할 때에는 Stop the world가 일어나서 어플리케이션이 잠깐동안 중단이 된다. 따라서 어플리케이션에 영향을 주지 않고 메모리가 full나지 않도록 하는 것이 목적이다.


객체와 GC 관계

1. 새롭게 생성된 객체는 Young generation의 eden에서 생성이 된다.

2. eden이 꽉차면 minor gc가 발생하고 이때 살아남은 친구들을 survivor1에 복사한다. 그리고 eden을 clear 한다.

3. 다음 eden에서 minor gc가 발생하면 survivor2에 복사하고 이때 survivor1에서 살아남은 친구들도 survivor2에 복사한다. 그리고 eden과 survivor2를 clear한다.

4. 이런 과정을 반복하면서 Young Gen에서 살아남은 친구들이 결국 Old Generation으로 복사가 된다.

즉 Young Generation(세부적으로 eden, survivor1, survivor2)과 Old Generation으로 나뉘는데 Young gen에서 발생하는 gc를 monir, Old gen에서 발생하는 gc를 full gc라고 부른다.

GC 종류마다 부르는 명칭은 다를지라도 청소하는 영역이 같다. (아래의 그래프에서 설명)
또한 suv1, suv2를 from, to 라고 불리기도 한다.




테스트할 GC는 CMS, G1GC 그리고 상용 GC인 ZING이다. ZING은 trial version으로 진행하였다.

테스트 하기전 설정을 살펴본다.

먼저 권장사항은 다음과 같다. 참고만하자.
출처 : Configuraing java heap space for cassandra

CMS 기준으로 설명해보면..
32G 시스템이므로 1/4크기만큼 주면 8G를 주기로 하였다.
MAX_HEAP_SIZE="8G"
HEAP_NEWSIZE="2G"


그리고 아래는 테스트 해가면서 조절해야한다.
-XX:NewRatio=2
-XX:SurvivorRatio=6
-XX:CMSInitiatingOccupancyFraction=75


위의 세팅을 해석해보자.
heap size가 8G인데 -XX:NewRatio=2이다. 즉 young:old 비율이 1:2이다. 만약 설정을 안하면 1:9가 default다.


young:old가 1:2이므로 8G를 배분하면 young이 약 2.6G, old가 5.3G을 가져간다.
-XX:CMSInitiatingOccupancyFraction=75이므로 75%가 찼을 때 GC 준비를 한다. 누군가 경험상으로 68%가 안전하다고 하는 글을 본적이 있지만 75%로 하였다.


XX:SurvivorRatio=6이므로 eden, suv1, suv2의 비율은 6:1:1이다. 따라서 young의 2.6G를 분배하면 1.95 : 0.325 : 0.325 가 된다.

G1GC나 ZING은 default 상태이다.

이제 본격적인 테스트를 해보자.
테스트 전 미리 원할한 jmx connection을 위해 아래와 같이 설정하였다.
authenticator: AllowAllAuthenticator
authorizer: AllowAllAuthorizer



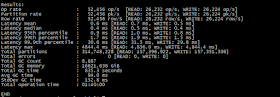
CMS GC mixed read/write test

./cassandra-stress mixed ratio\(write=1,read=1\) duration=100m -rate threads=\32 -node ip

concurrentmarksweep가 full gc라고 보면 되고 parnew가 minor gc라고 본다.

oncurrentmarksweep가 약 21회 호출되었고 used heap size가 약 6G가 넘을 때 호출되었다. 다행히 max heap size까지 차지는 않았다. 하지만 일부 gc 그래프에서 튀는 것을 확인할 수 있다.



G1GC mixed read/write test

./cassandra-stress mixed ratio\(write=1,read=1\) duration=100m -rate threads=\32 -node ip

G1 Old generation이 full gc이다. 약 15회 발생했다.
7G 근처에서 발생했고 튀지는 않지만 조금 더 다이나믹하게 gc가 일어난다.


ZING GC mixed read/write test

./cassandra-stress mixed ratio\(write=1,read=1\) duration=100m -rate threads=\32 -node ip

아무래도 ZING의 경우 상용 GC라서 더 좋긴 할텐데 그래프가 궁금했었다.
테스트 해본 결과 원하는 결과(ZING의 성능)가 막 높게 나오지 않아서 원인을 찾는 중이고.. 메모리를 더 주고 테스트를 해봐야할 것같다. 아무래도 메모리 관리 측면에서 봐야할 것 같다.

-> 추후 대용량 배치+과도한 트래픽으로 인해 장애가 났었는데 당시 ZING의 위엄(?)을 느낄 수 있었다. disk가 밀리고, network traffic이 밀리는 상황에도 카산드라 노드들은 zing을 통해 메모리 관리를 매우 잘하고 안정적인 상태를 보여주었다.
그런데 카산드라가 죽었을때 메모리 반환을 빨리 안할까봐 메모리를 쿼터만 주고 했는데 다음 테스트에서는 많이 줘봐야겠다.


현재 mixed 방식(write/read)를 테스트 했는데 각각의 경우에는 추후 포스팅에서 테스트 결과를 공유하도록 하겠다.
ZING의 메모리를 더 늘리고, 버전도 UP 시켜서 각각 테스트해볼 예정이다.



ZING을 테스트하면서 하나 느낀점은 cassandra가 죽었을 때, 혹은 재부팅할 때 메모리 반환을 바로 하지 않는다. 무언가 설정이 있을 것으로 보이지만 프로세스를 죽여도 zing이 기존에 잡고 있던 heap memory를 바로 반환하지 않는 것이 발견되었고 이는 장애가 났을 때 바로 어플리케이션을 살려야할 경우 메모리가 부족해서 안살아날 가능성이 있기 때문에 max heap memory size를 잘 조절 해야할것으로 보인다. 

Artificial Intelligence - The Maximum Entropy Method

만약 어떤 사건의 확률을 구해야한다면 베이즈 정리를 통해 어려운 확률도 쉽게 구할 수 있었다. 하지만 이는 주어진 지식이 충분할 때의 이야기이다.

만약 주어진 지식이 충분하지 않다면 베이즈 정리를 통한 접근이 어렵다.

이럴 땐 The Maximum Entropy Method을 통해 해결하는 방법이 있다.

The Maximum Entropy Method는 현재 주어진 정보를 갖고 가장 최선의 해를 찾는 최적화 방법 중의 하나로 Entropy는 정보가 전혀 없는 상태가 가장 높아 최대화가 된다. 즉 어떤 사건이 일어날 확률이 다른 사건들이 일어날 확률과 똑같다는 가정하에 확률을 구하는 방법이다.

α와β가 구해졌을 때 P(B)를 구해보자.

P(A,B) = (P(A,B), P(A,┐B), P(┐A,B), P(┐A,┐B)) 이다.
이를 아래처럼 치환하도록 하자
p1 = P(A,B)
p2 = P(A,┐B)
p3 = P(┐A,B)
p4 = P(┐A,┐B)

즉 p1+p2+p3+p4 = 1이다.

P(A,B) = P(B|A)P(A) = αβ (Chain rule에 의해)
P(A) = P(A,B) + P(A,┐B)) (Marginalization에 의해)

Chain rule과 Marginalization은 아래 포스팅을 참고한다.
https://parksuseong.blogspot.com/2019/12/artificial-intelligence-chain.html

더 나아가보자.
p1 = αβ
p1+p2 = α
p1+p2+p3+p4 = 1

p2 = α - αβ = α(1-β)
p3+p4 = 1-α

현재 주어진 지식으로는 여기까지 구하는 것이 최선이다.

Entropy를 적용해보는데 Entropy는 최대화하는 것이 목표이다.

P = (p3,p4)일 때 H(p)는 아래와 같다.
(H(P)는 로그값이 확률 값이므로 음수가 나오기 때문에 -를 해주는 것이다.)

이는 p3 + p4 = 1 - α 이고 p3 + p4 - 1 + α = 0이 된다.

Largange function L을 이용해서 아래처럼 정의하고 L을 maximize하자. (지식이 적으니까)

이를 통해 구하기 어려웠던 P(B)를 구할 수 있다.

P(B) = P(A,B) + P(┐A,B)
= p1 + p3
= αβ + (1-α/2)

정리를 하면 미지수가 4개인데 식이 3개이므로 방정식을 풀 수가 없었다.
하지만 최종적으로 p3 + p4 = 1 - α에서 두 개의 확률 변수 p3, p4로 하는 Joint 확률 분포 P(p3,p4)에서 entropy가 최대가 된다. 2개의 확률 변수 Entropy 함수는 H(P)로 주어진 식을 최대로 하는 값을 찾기 위해서 Largange function L을 편미분한 값이 0, 즉 최대임을 이용하면 식이 2개가 추가되므로(p3와 p4에 대한 식) 원래의 방정식을 풀 수 있다.

또한 H(P)는 로그값이 확률 값이므로 음수가 나오기 때문에 -(마이너스)를 해주는 것이다.

정보가 적을 때 Entropy가 최대가 된다. (이때 decision tree에서는 엔트로피의 차를 통해 Information gain을 구해서 decision 하게 된다.)

하지만 위의 문제를 maximum entropy를 적용하지 않고 사실 두 확률 변수의 확률을 1/2로 가정해서 풀어도 상관 없다. n개일때는 1/n으로 가정한다.

-
아주대 김민구교수님 강의를 바탕으로 작성합니다.

Artificial Intelligence - Bayes' Theorem (Alarm, Earthquake, Burglary Problem)

Bayesian network의 기반이 되는 Bayes' theorem에 대한 포스팅이다.
추후 베이지안 네트워크에 대해서 포스팅하려고 한다.

이 포스팅 전에 아래 포스팅을 참고하면 좋을 것이다.
https://parksuseong.blogspot.com/2019/12/artificial-intelligence-chain.html


우리는 조건부 확률 정의에 의해 P(A|B) = P(A∧B)/P(B) 와 P(B|A) = P(A∧B)/P(A) 임을 알고 있다.

Bayes' theorem은 P(A|B) = P(B|A) * P(A) / P(B) 이다.
풀어보면 B가 주어졌을 때 A의 확률은 A가 주어졌을 때 B가 일어날 확률 * A의 확률 / B의 확률이다.

즉 다음처럼 정리할 수 있다.

이러한 정의가 왜 필요할까?

맹장으로 진단할 확률 변수 App과 백혈구 수가 일정수준 이상일 확률을 나타내는 확률 변수를 Leuko라고 가정하자.

만약 실제상황에서 백혈구 수가 높은데 맹장염일 가능성을 추정해야하는 경우가 생기기 때문이다.

몇 가지의 지식이 미리 알려져있다면 구하기 어려운 확률을 구하는데 사용할 수 있다는 것이 Bayes's Theorem의 목표라고 할 수 있다.

즉, 맹장염일 때 백혈구의 수치는 높다가 아닌 백혈구 수치가 높을 때 맹장염일 확률을 구할 수 있다는 것이다.

위의 표에 의해서 만약 P(App|Leuko)를 구해야한다면 다음과 같다.

P(App|Leuko) = P(Leuko|App) * P(App) / P(Leuko) = 0.82 * 0.28 / 0.54 = 0.43이다.

다른 유명한 예를 살펴보자.

A : 알람(Alarm), E : 지진(Earth quake), B : 도둑(Burglary)
- 도둑이 들었을 때도 알람이 울린다.
- 도둑이 들었을 때는 알람이 울릴 확률은 99%이다.
- P(A|E) = 0.99 (지진이 났을 때 알람이 울릴 확률 99%)
- P(A) = 0.1 (알람이 울릴 확률은 10%이다.)
- P(E) = 0.001 (지진이 날 확률은 0.1%이다.)

이를 통해 알람이 울렸을 때 지진이 일어날 확률을 구해보자.
P(E|A) = P(A|E)P(E)/P(A) = 0.99 * 0.001 / 0.1 = 0.01

만약 도둑이 들 확률을 P(B) = 0.001로 가정해보자.
그렇다면 알람이 울렸을 때 도둑이 들 확률도 구할 수 있다.
P(B|A) = P(A|B)P(B)/P(A) = 0.99*0.001/0.1 = 0.01

이는 제시되어 알고 있는 지식 중에 도둑이 들었을 때 알람이 울릴 확률은 99%이지만 알람이 울렸을 때 도둑이 들었을 확률은 1%이다라는 것을 알 수 있다.

마무리를 하면 베이즈 정리(이론)은 이미 알고 있는 확률을 이용해서 복잡하거나 구하기 어려운 확률을 구하는데 사용되며 이는 Bayesian Network에서 원인과 결과를 그래프로 나타내는 실용적 모델에 사용되며 추후 포스팅하도록 하겠다.

Artificial Intelligence - Chain rule/Marginalization rule proof and example

Joint probability의 간단한 예로 P(A,B)는 A와 B가 각각 t,f일 경우의 수가 총 4개가 존재하며 이는 둘다 t일때 P(A,B) = P(A∧B)로 나타낼 수 있다. 그런데 만약 A,B 두 경우가 아닌 n개의 사건이 존재한다면 이는 차원의 갯수가 d라고 가정하여 n^d - 1의 경우를 계산해야한다. 이를 모두 계산하기란 사실상 불가능하다.

하지만 이런 Joint probabiliy를 간단하게 하는 방법이 몇 가지가 존재한다.

그 중에서 Chain rule과 Marginalization rule을 살펴보자.

Chain rule의 식은 다음과 같다.
Product rule : P(A∧B) = P(A|B)P(B)

이는 조건부 확률 P(A,B) = P(A|B)P(B)에 의해 증명이 가능하다.

P(X1,...Xn)
= P(Xn|X1,...,Xn-1) * P(X1,...,Xn-1)
= P(Xn|X1,...,Xn-1) * P(Xn-1|X1,...,Xn-2) * P(X1,...,Xn-2)
= P(Xn|X1,...,Xn-1) * P(Xn-1|X1,...,Xn-2) * ... * P(X2|X1) * P(X1)
= ∏ P(Xi|X1,...,Xi-1)


Marginalization rule은 다음과 같다. A와 B는 binary 하다.
P(A) = P((A∧B) ∨ (A∧┐B)) = P(A∧B) + P(A∧┐B)
A가 일어날 확률은 B가 일어났을 경우/일어나지 않았을 경우의 확률의 합이다.

이를 일반화해보자.
P(X1 = x1,...,Xd-1 = xd-1) = ΣP(X1 = x1,...,Xd-1 = xd-1, Xd = xd)
즉 우측을 확률을 다 더하면 좌측의 확률이 나온다는 것이다.

정리하면 한개의 확률 변수의 모든 경우의 수를 모두 합치면 그 변수를 사용하지 않는 것과 같다는 것이다.

Marginalization rule의 예를 들어보자.

맹장으로 진단할 확률 변수 App과 백혈구 수가 일정수준 이상일 확률을 나타내는 확률 변수를 Leuko라고 가정하자.
P(Leuko|App)는 맹장으로 진단했을 때 백혈구 수가 일정수준 이상일 확률이다.

제시된 표에 의해 P(Leuko) = 0.54이고, P(App) = 0.28이다.
따라서 P(Leuko|App)는 P(Leuko,App) / P(App)이고 0.23/0.28 = 0.82가 된다.